SPDE Gallery

Exploring the visual beauty of Stochastic Partial Differential Equations

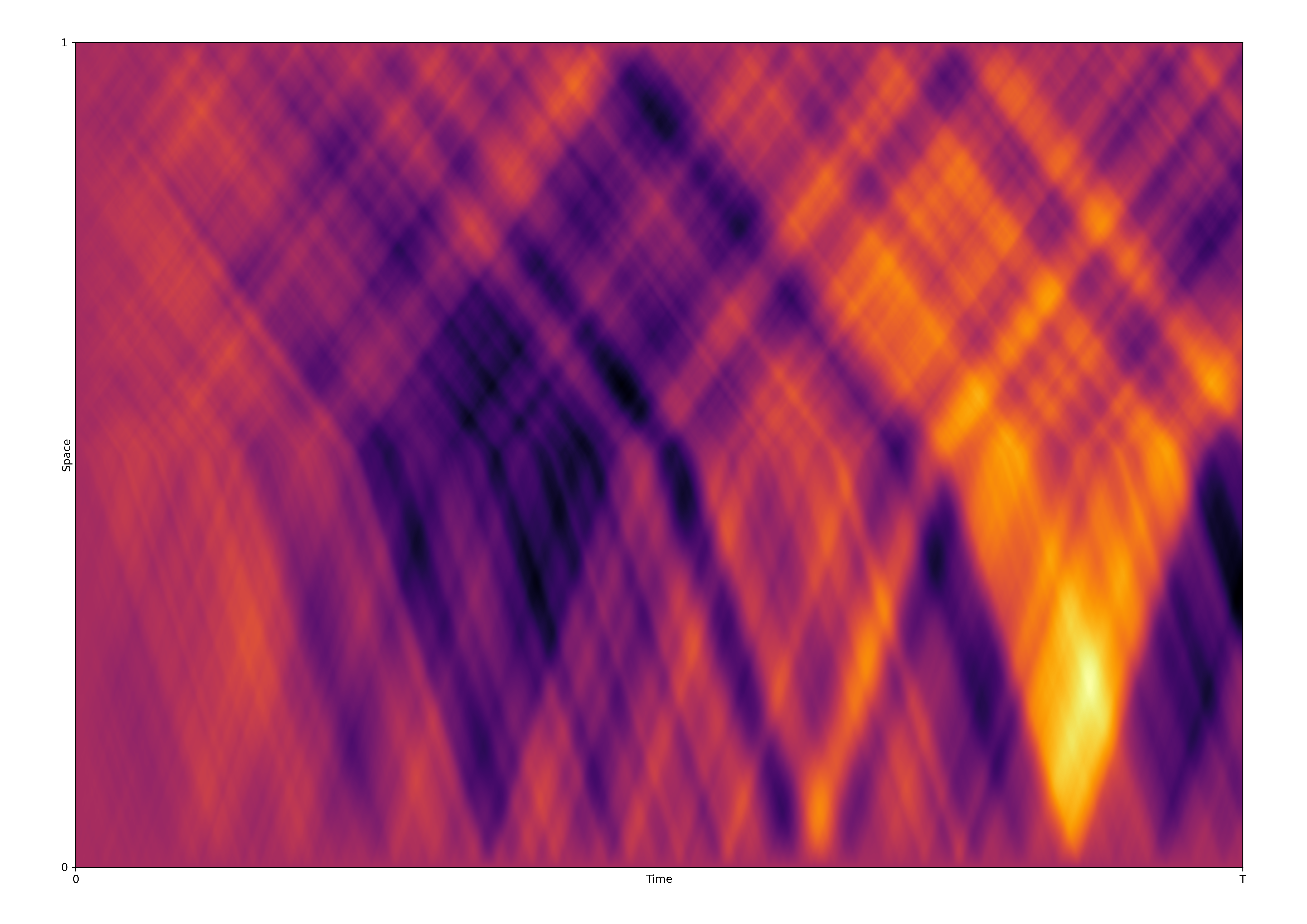
Stochastic wave equation with spatially dependent speed

Stochastic wave equation with spatially dependent speed

The estimation of the wave speed ϑ\vartheta using local measurements is intrinsically related to the energetic behaviour of the wave equation and involves the theory of Riemann-Lebesgue operators. Heatmap with ϑ(z)=ϑ01[0,0.5](z)+ϑ11(0.5,1](z),z∈[0,1].\vartheta(z)= \vartheta_0 \mathbf{1}_{[0,0.5]}(z)+ \vartheta_1 \mathbf{1}_{(0.5,1]}(z),z \in [0,1].
Stochastic Allen-Cahn equation with time-varying diffusivity

Stochastic Allen-Cahn equation with time-varying diffusivity

The estimation of the reaction function ϑ\vartheta uses the asymptotic spatial ergodicity of the system as the diffusivity tends to zero and requires Malliavin calculus. Heatmap with ϑ(z)=−4(z3−16z)\vartheta(z) = -4(z^3-16z) for z∈Rz\in\mathbb{R}, σ=1\sigma = 1 and ν(t)=10(−0.6t−2)\nu(t) = 10^{(-0.6t-2)}.
Activator component of a stochastic FitzHugh-Nagumo system with mass stabilisation

Activator component of a stochastic FitzHugh-Nagumo system with mass stabilisation

The estimation of the activator diffusivity turns out to be asymptotically robust under misspecification in the reaction model in the generating equations. This can even encompass the presence or absence of different dynamical features in the observed trajectory.
Stochastic heat equation with multiplicative noise

Stochastic heat equation with multiplicative noise

Under multiplicative noise, the standard local estimator of ϑ\vartheta is asymptotically mixed normal as the resolution becomes finer. This is based on Brownian martingale representation in Hilbert spaces and stable convergence. Weighting by quadratic variation improves the estimator and enjoys asymptotic normality. Heatmap with ϑ=0.20\vartheta = 0.20, σ(z)=0.20×∣z∣0.8+0.01\sigma(z) = 0.20 \times |z|^{0.8} + 0.01.
Stochastic Allen-Cahn equation with noise and space-dependent Hurst parameter

Stochastic Allen-Cahn equation with noise and space-dependent Hurst parameter

Estimation of the Hurst parameter HH in parabolic SPDEs can be based on exploiting the local effect of parabolic spatio-temporal scaling on the probabilistic distribution of the space-time noise via its self-similarity. Heatmap with H(x)=xH(x) = x and ϑ(z)=40z(1−z)(z−1/2)\vartheta(z)=40 z (1-z)(z-1/2).
Stochastic convection-diffusion equation with spatial transport

Stochastic convection-diffusion equation with spatial transport

To estimate the spatially varying transport coefficient of a stochastic convection-diffusion equation, the contribution of different local measurements must be weighted and controlled by a bandwidth to account for bias reduction. Heatmap with a=0.02a=0.02, c=0.3c=0.3 and ϑ(z)=−0.5−3z2\vartheta(z)=-0.5-3z^2 for z∈[0,1]z \in [0,1].